Neychapour

Iran : les Incontournables de (d') > Ailleurs en Iran

NOS CIRCUITS INCONTOURNABLES & PERSONNALISABLES EN IRAN

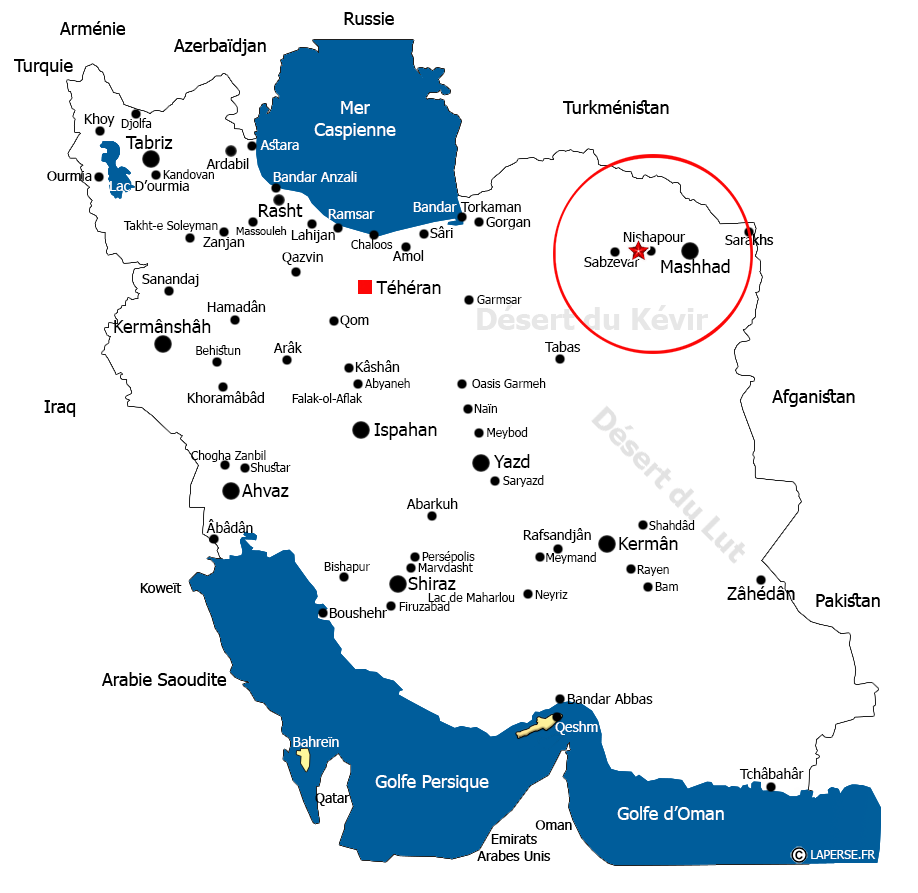
Nishapur, Nichapour ou Neishabur est une des principales villes de la région du Khorassan-e Razavi, au nord-est de l'Iran.

Histoire

La ville est fondée sous les Sassanides au iii^e siècle par Chapour I^er avant d'être reconstruite par Chapour II, d'où son nom de Nev-Shabur, "Nouvelle Shabur".

Un évêché nestorien y est établi au v^e siècle.

Elle est occupée par les Arabes en 651. Les révoltes ne sont pacifiées qu'en 692.
Sous la dynastie des tahirides, elle devient la capitale du Khorasan.
En 901, elle tombe aux mains des Samanides.
Des tremblements de terre la détruisent.
Elle est la capitale des Seldjoukides en 1037.
En septembre 1208, un tremblement de terre la touche gravement.
Les Mongols des hordes de Genghis Khan la mettent à sac en avril 1221 et exterminent sa population. Des rumeurs non fondées font état de la mort de 1 748 000 personnes (dont peut-être le poète soufi Farid al-Din Attar), ce qui est vraisemblablement exagéré.
D'autres séismes la détruisent ; celui de 1270 contraint la population à rebâtir la cité sur un autre site.
Elle est éclipsée comme capitale régionale par la ville sainte de Mashhad.

Nishapur fut l'une des villes les plus prospères de l'Orient musulman jusqu'à l'époque mongole. Elle conserve une certaine importance économique en raison de ses mines de turquoise et de son agriculture (fruits, coton, céréales).

Monuments

Tombeau d'Omar Khayyam ;
Tombeau de Farid Al-Din Attar ;
Tombeau d'Abū ‘Uthmān al-Maghribī.

Personnalités

Abû 'Abd ar-Rahmân as-Sulamî (x^e siècle), historien du soufisme.
Muslim ben al-Hajjaj, auteur du célèbre recueil de hadiths éponyme.
Hakim al-Nishaburi, célèbre muhaddith.
as-Sulami, mystique soufi.
Abû Ḥamid al-Ghazālī (1058-1111), soufi et théologien islamique.
Omar Khayyām, écrivain, mathématicien et astronome perse.
Farid Al-Din Attar, mystique de l'Islam et poète perse, à qui Jalal Ud Din Rumi a rendu visite vers 1219 à Nichapur.
Haci Bektas Veli, mystique et philosophe du xiii^e siècle
Mohammad Reza Shafiei-Kadkani, poète, écrivain et professeur de littérature persane, connu pour ses critiques littéraires.
Ostad Parviz Meshkatian, célèbre compositeur et joueur de santour.
Heydar Yaghma, poète illettré qui a publié ses œuvres.
Ostad Djalal Akhbari, grand compositeur et joueur de santour.

OMAR KHAYYAM

Omar Khayyām (v. 1048? à Nichapur en Perse (actuel Iran) - v. 1131) est un poète et savant persan. On trouve son nom orthographié Omar Khayam dans les traductions d'Armand Robin (1958) ou de M. F. Farzaneh et Jean Malaplate (dans l'édition critique de Sadegh Hedayat, Corti, 1993). Sa date de naissance est supposée. Ses poèmes sont principalement écrits en persan alors que ses traités scientifiques le sont en arabe.

Biographie

La vie de Khayyam est entourée de mystère, et la rareté des sources disponibles empêche de la retracer avec précision. Des chercheurs pensent généralement qu’Omar Khayyam est né dans une famille d'artisans de Nichapur — le nom de Khayyam, du persan خيام [ḫayām], en arabe خَيَّميّ [ḫayyamī] : fabricant de tentes, suggère que son père était fabricant de tentes.

Omar Khayyām
Date/Lieu de naissance : 18 mai 1048, Nishapur, Iran Date de décès : 4 décembre 1131, Nishapur, Iran Lieu d'inhumation : Mausolée d'Omar Khayyam, Iran Influences : Avicenne, Al-Biruni, Al-Khwârizmî, Alhazen, Euclide, Apollonios de Perga Parents : Ibrahim Khayyam Nayshapuri Personne Influencée : Edward FitzGerald, Sadegh Hedayat, André Gide

Il passe son enfance dans la ville de Balhi, où il étudie sous la direction du cheik Mohammad Mansuri, l'un des savants les plus célèbres de son temps (selon le vizir Nizam al-Mulk dans son "wasiyat", son testament). Dans sa jeunesse, Omar Khayyām étudie aussi sous la direction de l'imam Mowaffak de Nishapur, considéré comme le meilleur professeur du Khorassan.

En 1074, il est invité par le sultan seldjoukide Mālikshāh Jalāl al-Dīn à Ispahan pour entreprendre la réforme du calendrier solaire à laquelle il consacrera cinq années, et organiser des observations astronomiques.

À la mort de Mālikshāh, il tombe en disgrâce. Il est possible que certains de ses poèmes non orthodoxes en soient la cause. Pour couper court à tout soupçon, il entreprend alors un pèlerinage à la Mecque. On le retrouve ensuite à Merv, alors capitale de l'empire des Seldjoukides. Il finit ses jours à Nichapur, où il vit en reclus les vingt dernières années de sa vie.

Nom de Khayyam

Si on le déchiffre avec le système abjad, le résultat donne al-Ghaqi, le dissipateur de biens, expression qui dans la terminologie soufie est attribuée à « celui qui distribue ou ignore les biens du monde constituant un fardeau dans le voyage qu'il entreprend sur le sentier soufi » (Omar Ali-Shah).

« Khayyam, qui cousait les tentes de l'intelligence,
Dans une forge de souffrances tomba, subitement brûla ;
Des ciseaux coupèrent les attaches de la tente de sa vie ;
Le brocanteur de destins le mit en vente contre du vent. »

Mathématicien et astronome

Omar Khayyâm est considéré comme « l'un des grands mathématiciens du Moyen Âge. » Mais ses travaux algébriques ne furent publiés en Europe qu'au xix^e siècle.

On lui doit deux traités importants dans l'histoire des mathématiques.

Dans son Risāla fī’l-barāhīn ˓ala masā’il al-jabr wa’l-muqābala (Démonstrations de problèmes d'algèbre) écrit en 1070 à Samarcande et dédié à son protecteur le juge Abu Tahir, al-Khayyam entreprend une classification des équations de degré trois avec leurs racines positives. Il échoue dans sa tentative de résoudre ces équations par radicaux mais il décrit le moyen d'obtenir ces racines à l'aide d'intersection de coniques (cercles, hyperboles équilatères, paraboles). Il démontre que les équations cubiques peuvent avoir plus d’une racine. Il fait état aussi d’équations ayant deux solutions, mais n'en trouve pas à trois solutions.

Son deuxième traité Sharh. mā ashkala min mus.ādarāt kitāb Uqlīdis (Commentaires sur les difficultés de certains postulats du livre d'Euclide) écrit en 1077 à Ispahan offre une réflexion sur l'axiome des parallèles. Son raisonnement s'appuie sur un quadrilatère dont les deux angles de base sont droits, et les côtés latéraux de même longueur. Le but est de démontrer que les deux autres angles ne sont ni aigus ni obtus. Ce même quadrilatère sera repris plusieurs siècles plus tard par le mathématicien Giovanni Girolamo Saccheri. On trouve également dans ce traité des réflexions sur les fractions.

À ces deux ouvrages, on peut ajouter un Traité sur la division d'un quart de cercle dans lequel al-Khayyam détermine la valeur approchée d'une racine d'une équation cubique et un traité Problème d'arithmétique cité par ses successeurs et qui devait contenir des méthodes des binômes et de calculs approchés de racines nièmes.

Directeur de l'observatoire d'Ispahan en 1074, il réforme, à la demande du sultan Malik Shah, le calendrier persan (la réforme est connue sous le nom de réforme djelaléenne). Il construit des tables astronomiques connues sous le nom de Zidj-e Malikshahi.

Il introduit à la manière du calendrier julien une année bissextile et mesure la longueur de l’année comme étant de 365,242 198 jours. L'estimation djélaléenne se montrera plus exacte que la grégorienne créée cinq siècles plus tard, bien que leur résultat pratique soit exactement le même, une année devant comporter un nombre entier de jours.

Dans le domaine de la physique, al-Khayyam s'est intéressé au problème de la balance et de la détermination de la composition des alliages (Fī ikhtiyāl ma˒rifa miqdāray al-dhahab wa’l-fid.d.a fī jism murakkab minhumā - Sur l'art de déterminer la quantité d'or et d'argent dans un corps constitué de ces deux matières et Fī’l-qustās. al-mustaqīm - Sur la balance). Ses traités seront repris par son élève à Merv, al-Khazini, (Fī’l-qustās.al-mustaqīm Le livre de la balance de la sagesse).

Al-Khayam a également écrit un traité sur les divisions de gammes musicales.

Poète et philosophe

Ses poèmes sont appelés « rubaiyat », ce qui signifie « quatrains ». Les quatrains de Khayyam, souvent cités en Occident pour leur scepticisme, recèleraient, selon Idries Shah, des « perles mystiques », faisant de Khayyam un soufi. Il aurait prôné l'ivresse de Dieu, et se disait infidèle mais croyant. Au-delà du premier degré hédoniste, les quatrains auraient donc selon ce commentateur une dimension mystique.

Dans la pratique, si l'on s'en tient au texte, Khayyam se montre bel et bien fort critique vis-à-vis des religieux — et de la religion — de son temps. Quant au vin dont la mention revient fréquemment dans ses quatrains, le contexte où il se place constamment (agréable compagnie de jeunes femmes ou d'échansons, refus de poursuivre la recherche de cette connaissance que Khayyam a jadis tant aimée) ne lui laisse guère de latitude pour être allégorique.

On ne peut donc que constater l'existence de ces deux points de vue.

Traduction de Franz Toussaint pour les quatrains ci-après.

Chagrin et désespoir

« En ce monde, contente-toi d'avoir peu d'amis.
Ne cherche pas à rendre durable
la sympathie que tu peux éprouver pour quelqu'un.
Avant de prendre la main d'un homme,
demande-toi si elle ne te frappera pas, un jour. »

« Tu peux sonder la nuit qui nous entoure.
Tu peux foncer sur cette nuit... Tu n'en sortiras pas.
Adam et Ève, qu'il a dû être atroce, votre premier baiser,
puisque vous nous avez créés désespérés ! »

Lucidité et scepticisme

« Contente-toi de savoir que tout est mystère :
la création du monde et la tienne,
la destinée du monde et la tienne.
Souris à ces mystères comme à un danger que tu mépriserais. »

« Ne crois pas que tu sauras quelque chose
quand tu auras franchi la porte de la Mort.
Paix à l'homme dans le noir silence de l'Au-Delà ! »

Sagesse et épicurisme

« Au printemps, je vais quelques fois m'asseoir à la lisière d'un champ fleuri.
Lorsqu'une belle jeune fille m'apporte une coupe de vin, je ne pense guère à mon salut.
Si j'avais cette préoccupation, je vaudrais moins qu'un chien. »

« Luths, parfums et coupes,
lèvres, chevelures et longs yeux,
jouets que le Temps détruit, jouets !
Austérité, solitude et labeur,
méditation, prière et renoncement,
cendres que le Temps écrase, cendres ! »

C'est sur cette 170^e pièce, comme en conclusion de ce qui précède, que se termine le recueil.

Distance par rapport à l'islam orthodoxe

« Autrefois, quand je fréquentais les mosquées,
je n'y prononçais aucune prière,
mais j'en revenais riche d'espoir.
Je vais toujours m'asseoir dans les mosquées,
où l'ombre est propice au sommeil. »

« « Allah est grand ! » Ce cri du moueddin ressemble à une immense plainte.
Cinq fois par jour, est-ce la Terre qui gémit vers son créateur indifférent ? »

« Puisque notre sort, ici-bas, est de souffrir puis de mourir,
ne devons-nous pas souhaiter de rendre le plus tôt possible à la terre notre corps misérable ?
Et notre âme, qu'Allah attend pour la juger selon ses mérites, dites-vous ?
Je vous répondrai là-dessus quand j'aurai été renseigné par quelqu'un revenant de chez les morts. »

Notoriété universelle et image ambigüe

Les agnostiques voient en lui un de leurs frères né trop tôt, tandis que certains musulmans perçoivent plutôt chez lui un symbolisme ésotérique, rattaché au soufisme.

Khayyam indiquerait, comme le fera Djalâl ad-Dîn Rûmî plus tard, que l'homme sur le chemin de Dieu n'a pas besoin de lieu dédié pour vénérer celui-ci, et que la fréquentation des sanctuaires religieux n'est ni une garantie du contact avec Dieu, ni un indicateur du respect d'une discipline intérieure.

L'actuelle république islamique d'Iran ne nie pas les positions de Khayyam, mais a fait paraître au début des années 1980 une liste officielle des quatrains qu'elle considérait comme authentiques (comme pour les Pensées de Pascal, leur nombre et leur numérotation diffèrent selon les compilateurs).

La vision d'un Khayyam ésotériste n'est pas partagée par ceux qui voient en lui surtout un hédoniste tolérant et sceptique. En effet, si certains assimilent dans ses poèmes le vin à une sorte de manne céleste, d'autres comme Sadegh Hedayat considèrent plutôt le poète comme un chantre de la liberté individuelle, qui refuse de trancher sur des mystères lui semblant hors de portée de l'homme.

Son appréciation simple des plaisirs terrestres après la quadruple déception de la religion (quatrains 25, 76, 141), des hommes (quatrains 8, 18, 33) de la science (quatrains 26 à 30, 77, 81) et de la condition humaine elle-même (quatrains 32, 67, 107, 120, 170) n'exclut aucune hypothèse (quatrains 1, 23 à 25, 52).

Si chacune des deux interprétations est controversée par les tenants de l'autre, elles ne s'excluent cependant pas nécessairement : Khayyam présente sans ordre et sans méthode, pour reprendre une expression de Montaigne dans la préface des Essais - donc sans stratégie visant à convaincre - ses espoirs, ses doutes et ses découragements dans ce qui semble un effort de vérité humaine. C'est peut-être une des raisons du succès mondial des quatrains.

Traductions

Controverses autour des manuscrits et des traductions

La diversité des manuscrits et le problème de leur authenticité, ainsi que la nécessité de connaître la langue et la civilisation perses du onzième siècle montrent les difficultés d'une traduction. Marguerite Yourcenar dit à ce propos : « Quoi qu'on fasse, on reconstruit toujours le monument à sa manière. Mais c'est déjà beaucoup de n'employer que des pierres authentiques ». Armand Robin dresse une liste de ces pierres dans Ce qu'en 1958 on peut savoir sur les « quatrains » d'Omar Khayam lors de sa traduction (cf. Bibliographie).
- Manuscrit de 1460 de la Bibliothèque bodléienne d'Oxford, soit 158 quatrains traduits, en anglais par FitzGerald (1859), en français par Charles Grolleau (1909). Une centaine de ces quatrains sont incertains.
- Manuscrit de 464 quatrains traduits en français par J.-B. Nicolas (1861).
- Manuscrit d'Istanbul, 375 quatrains étudiés fin XIX^e début xx^e siècle
- Manuscrit de Lucknow, 845 quatrains étudiés fin XIX^e début xx^e siècle
- Manuscrit de 1259 dit de « Chester-Beatty », du scribe Mohammed al Qâwim de Nichapour, 172 quatrains traduits en français par Vincent Monteil (1983).
- Manuscrit de 1207 dit de « Cambridge », acheté en 1950. Anthologie de 250 quatrains traduits par Arthur John Arberry (1952, il avait expertisé le manuscrit « Chester-Beatty »).
- Manuscrit de 1153 découvert « dans une immense bibliothèque familiale », 111 quatrains traduits en anglais par Omar Ali-Shah « de langue maternelle persane, soufi… » (1964).
Traductions et interprétations.

Le fait que les rubaiyat soient un recueil de quatrains — qui peuvent être sélectionnés et réarrangés arbitrairement et suggérer ainsi telle interprétation ou telle autre — a mené à des versions qui diffèrent grandement. J.-B. Nicolas a pris le parti de dire que Khayyam se considère clairement comme un soufi. D'autres y ont vu des signes de mysticisme, ou même d'athéisme, et d'autres au contraire le signe d'un Islam dévot et orthodoxe.

FitzGerald a donné au Rubaiyat une atmosphère fataliste, mais s'il est dit qu'il a adouci l'impact du nihilisme de Khayyam et de ses préoccupations de la mort et du caractère transitoire de toutes choses. La question de savoir si Khayyam était pour ou contre la consommation de vin est elle-même controversée, celle-ci et l’ivresse qui en découle ayant un sens métaphorique dans le soufisme.

Dans la nouvelle traduction que Jean-Yves Lacroix, dans Le cure-dent, fait des quatrains « Rubaï'yat », qualifiés de « serpent venimeux pour la loi divine », par le chroniqueur al-Qifti, Khayyam écrit : « Tout le monde sait que je n'ai jamais murmuré la moindre prière », et ailleurs ceci : « Referme ton Coran. Pense librement et regarde librement le ciel et la terre. »

Les quatrains de Khayyâm font l'objet de quelques controverses de traduction ainsi que d'éditions. En Europe, FitzGerald et Toussaint sont les références les plus courantes. Il est cependant difficile, comme dans toute traduction poétique, de rendre tout le sens original des vers. Le sens mystique de cette poésie peut échapper au non-spécialiste. Quant à FitzGerald, il combine parfois des quatrains distincts pour rendre possible une rime (Toussaint, mécontent de la traduction de FitzGerald, préfère une prose à laquelle il donne un souffle poétique).

Le contenu original du recueil de quatrains de Kayyâm est aussi soumis à de vastes débats. En effet, la tradition attribue plus de 1 000 quatrains à Khayyam ; alors que la plupart des chercheurs ne lui en attribuent avec certitude que 50, avec environ 200 autres quatrains soumis à controverse. Chez Toussaint et FitzGerald, le nombre est de 170.

Le gouvernement iranien a fait paraître dans les années 1980 la liste des quatrains qu'il reconnait officiellement.

Découverte d'Omar Khayyâm en Occident grâce aux traductions d'Edward FitzGerald

Ce fut la traduction anglaise d'Edward FitzGerald qui fit connaître au grand public, en 1859, l'œuvre poétique de Khayyam et qui servit de référence aux traductions dans beaucoup d'autres langues.

FitzGerald dut effectuer un choix parmi les mille poèmes attribués à Khayyam par la tradition, car le genre littéraire qu'il avait inauguré avait connu un tel succès que l'on employait le terme générique khayyam pour désigner toute lamentation désabusée sur la condition humaine. FitzGerald établit quatre éditions des quatrains comprenant entre 75 et 110 quatrains. Étonnamment, c'est encore souvent une des compilations établies par FitzGerald qui sert de référence à une grande partie des autres traductions.

Les traductions de FitzGerald sont encore très discutées, notamment en ce qui concerne leur authenticité, FitzGerald ayant profité de ces traductions pour réécrire totalement des passages hors de l'esprit du poète original, comme la plupart des traducteurs de l'époque le faisaient. Ainsi, Omar Ali-Shah prend l'exemple du premier quatrain afin de montrer les étonnantes divergences de sens entre la traduction anglaise et la traduction littérale française.

Traduction du persan en français de l'orientaliste Franz Toussaint

L'orientaliste français Franz Toussaint préféra effectuer une nouvelle traduction à partir du texte original persan plutôt qu'à partir de l'anglais, avec le parti-pris de ne pas chercher à traduire les quatrains en quatrains, mais dans une prose poétique qu'il estimait plus fidèle.

Sa traduction française, composée de 170 quatrains, a été contestée par les uns, défendue par d'autres avec vigueur. Aujourd'hui, après la disparition des Éditions d'art Henri Piazza qui l'ont largement diffusée entre 1924 et 1979, cette traduction fait elle-même l'objet de traductions dans d'autres langues. Toussaint, décédé en 1955, n'a pas été témoin de ce succès.

Dilemme des traducteurs

Quelques quatrains semblent échapper à toute traduction définitive, en raison de la complexité de la langue persane. Ainsi, Khayyam mentionne un certain Bahram (probablement Vahram V Gour) qui de son vivant prenait grand plaisir à attraper des onagres (Bahram ke Gour migerefti hame 'omr) et ajoute laconiquement que c'est la tombe qui a attrapé Bahram. Les mots onagre et tombe sont phonétiquement voisins en persan, avec une phonie ressemblant à gour (Didi keh chegune gour bahram gereft).

Le poète Robert Graves publia en 1967 une traduction en anglais, jugée discutable, de 111 quatrains d'Omar Khayyam.

L'édition récente de la traduction française des quatrains par Omar Ali-Shah critique la plupart des traductions antérieures, à commencer par celle de FitzGerald ou certaines traductions françaises.

Selon Omar Ali-Shah, le persan des quatrains de Khayyâm se réfère constamment au vocabulaire soufi et a été injustement traduit dans l'oubli de sa signification spirituelle. Ainsi il affirme que le « Vin » de Khayyâm est un vin spirituel, que la Tariqa est la Voie (sous entendue au sens soufi de chemin mystique vers Dieu) et non la « route » ou « route secondaire », présente selon lui dans certaines traductions (il ne précise pas lesquelles).

Néanmoins les quatrains laissant paraître un scepticisme désabusé ne trouvent dans cette optique aucune explication. Cette interprétation mystique est également celle proposée par Paramahansa Yogananda dans The wine of the mystic, reprenant la traduction anglaise d'Edward FitzGerald, avec un commentaire de chaque quatrain.

Quelques quatrains

« Hier est passé, n’y pensons plus
Demain n’est pas là, n’y pensons plus
Pensons aux doux moments de la vie
Ce qui n’est plus, n’y pensons plus »

« Ce vase était le pauvre amant d’une bien-aimée
Il fut piégé par les cheveux d’une bien-aimée
L’anse que tu vois, au cou de ce vase
Fut le bras autour du cou d’une bien-aimée! »

« Elle passe bien vite cette caravane de notre vie
Ne perds rien des doux moments de notre vie
Ne pense pas au lendemain de cette nuit
Prends du vin, il faut saisir les doux moments de notre vie »

— Dictionnaire des poètes renommés persans : À partir de l'apparition du persan dari jusqu'à nos jours (trad. Mahshid Moshiri), Téhéran, Aryan-Tarjoman, 2007.

« Les astres à ma présence ici‐bas n’ont rien gagné, Leur gloire à ma déchéance ne sera pas augmentée; Et, témoin mes deux oreilles, nul n’a jamais pu me dire Pourquoi l’On m’a fait venir et l’On me fait m’en aller. »

— Quatrain dans la traduction de M. Gilbert Lazard («Cent un Quatrains», éd. La Différence, coll. Orphée, Paris)

Khayyâm l'inspirateur

Omar Khayyâm, depuis sa découverte en Occident, a exercé une fascination récurrente sur des écrivains européens comme Marguerite Yourcenar, qui confessait : une « autre figure historique [que celle de l'empereur Hadrien] m'a tentée avec une insistance presque égale : Omar Khayyam... Mais [sa] vie... est celle du contemplateur, et du contempteur pur » tout en ajoutant, « d'ailleurs, je ne connais pas la Perse et n'en sais pas la langue ».

Il inspira aussi le roman Samarcande d'Amin Maalouf.

Musicalement, il inspira également les compositeurs suivants :

sir Granville Bantock : Omar Khayyam, grande symphonie pour solistes, chœurs et orchestre
Jean Cras : Roubayat, cycle de mélodies.
Sofia Goubaïdoulina : Roubayat, cycle de mélodies.
Camarón de la Isla : Viejo Mundo, composée par Kiko Veneno à partir de fragments du Rubaiyat, dans le disque La leyenda del tiempo (1979).
Tony Gatlif : hommage à Omar Khayyâm, Festival des musiques sacrées de Fès, 2012
Le groupe Mauresca Fracàs Dub et son titre Omar Khayyam présent sur l'album Riòta (sorti en 2014)
Rockin' Squat dans son titre « le savoir est une arme » y fait référence dans la phrase suivante : « Comme Omar Khayyam je trouverai la sagesse ».
Dorothy Ashby : The Rubhaiyat of Dorothy Ashby, 1970.

Le poète-parolier égyptien Ahmed Rami a créé pour Om Kalthoum un chant inspiré de Rubaiyat el-Khayyam qui fut mis en musique par Riadh Sombati, en 1951. Cette chanson dite Rubaiyat el-Khayyam [archive] est considérée par les puristes comme étant une des trois meilleures chansons d'Om Kalthoum.

Il inspira encore des poètes qui à leur tour écrivirent des rubaiyat :

Fernando Pessoa, Rubaiyat (quatrains).
Yéghiché Tcharents, Rubaiyat (poèmes de la pensée).
Bernard Lavilliers dans son album Les poètes débute la chanson Femme par un poème de Khayyâm : « Un peu de pain, un peu d’eau fraîche, l’ombre d’un arbre, et tes yeux ! Aucun sultan n’est plus heureux que moi. Aucun mendiant n’est plus triste ».

Hommages

Un cratère lunaire a été baptisé de son nom en 1970.
L'astéroïde (3095) Omarkhayyam a été nommé en son honneur en 1980.
Un voilier classique classé monument historique porte son nom.

Dans la culture populaire

Au cinéma et dans les séries télévisées

Les films Pandora et Le portrait de Dorian Gray de Albert Lewin s'ouvrent par des citations de quatrains de Omar Khayyam.
Dans le film Poulet aux prunes réalisé par Marjane Satrapi et Vincent Paronnaud il y a une référence à un quatrain de Omar Khayyam (« Les astres à ma présence ici-bas n’ont rien gagné...»)
Dans l'épisode 16 de la saison 3 de la série The Big Bang Theory, le personnage de Sheldon Cooper fait référence à Omar Khayyam en citant : « The Moving Finger writes; and, having writ, moves on ».

Dans la littérature[

Le quatrain du Doigt mouvant a inspiré à l’écrivaine Agatha Christie le titre d’un de ses romans policiers : The Moving Finger, paru en traduction française sous le titre de La Plume empoisonnée.
Le même quatrain du Doigt mouvant est cité partiellement dans le roman Manhattan Transfer de John Dos Passos, aux premières pages du chapitre II (« Nickelodeon ») de la 3^e partie (à la page 363 de l’edition de poche Folio).
Le roman historique Samarcande de l'écrivain libanais Amine Maalouf traite des circonstances de l'écriture des quatrains de Omar Khayyam, puis de la quête du manuscrit qu'a laissé le poète persan.

Bibliographie

Notice d'autorité d'Omar Khayyam

Notices d'autorité :

Fichier d’autorité international virtuel
International Standard Name Identifier
CiNii
Bibliothèque nationale de France (données)
Système universitaire de documentation
Bibliothèque du Congrès
Gemeinsame Normdatei
Service bibliothécaire national
Bibliothèque nationale de la Diète
Bibliothèque nationale d’Espagne
Bibliothèque royale des Pays-Bas
Bibliothèque nationale de Pologne
Bibliothèque nationale d’Israël
Bibliothèque universitaire de Pologne
Bibliothèque nationale de Suède
Bibliothèque apostolique vaticane
Autorités Canadiana
Bibliothèque nationale d’Australie
WorldCat

Œuvres poétiques

Omar Khayyâm, Les Rubâ'iyat, adaptation du persan par Pierre Seghers, Éditions Seghers, 1979
L'Amour, le désir, & le vin. Omar Khâyyâm (60 poèmes sur l'Amour et le Vin), calligraphies de Lassaad Métoui. Paris, Alternatives, 2008, 128p.
Les Quatrains d'Omar Khâyyâm, traduits de l'anglais et présentés par Charles Grolleau, Ed. Charles Corrington, 1902. (Rééd. éditions Champ libre / Ivrea, 1978). (Rééd. éditions 1001 Nuits, 79p., 1995). (Rééd. éditions Allia, 2008).
Rubayat Omar Khayam, traduction d'Armand Robin (1958), (Rééd. Préf. d'André Velter, Poésie/Gallimard, 109p., 1994, (ISBN 207032785X)).
Quatrains Omar Khayyâm suivi de Ballades de Hâfez, poèmes choisis, traduits et présentés par Vincent Monteil, bilingue Calligraphies de Blandine Furet, 171p., Coll. La Bibliothèque persane, Ed. Sindbad, 1983.
Les Chants d'Omar Khayyâm, édition critique de Sadegh Hedayat, traduite du Persan par M. F. Farzaneh et Jean Malaplate, Éditions José Corti, 1993.
Quatrains d'Omar Khayyâm, édition bilingue, poèmes traduits du persan par Vincent-Mansour Monteil, Éditions Actes Sud, Collection Babel, 1998. (ISBN 2-7427-4744-3).
Cent un quatrains de libre pensée d'Omar Khayyâm, édition bilingue, traduit du persan par Gilbert Lazard, Éditions Gallimard, Connaissance de l'Orient, 2002. (ISBN 978-2-07-076720-5).
Les Quatrains d'Omar Khayyâm, traduction du persan & préf. d'Omar Ali-Shah, trad. de l'anglais par Patrice Ricord, Coll. Spiritualités vivantes, Albin Michel, 146p., 2005, (ISBN 2226159134).
"Poètes de l'ivresse et du vin. Omar Khayam, Li Po, Charles Baudelaire", Michel Antoni, L'Harmattan, 2019

Œuvres philosophiques

Un traité de métaphysique de Omar Hayyâm [archive], A. Christensen, introduction et traduction d'un manuscrit inédit, in le Monde Oriental, vol. 1-2, Uppsala, 1906.

Œuvres mathématiques

Voir aussi la bibliographie des Irem (France).

Traité sur l'algèbre (vers 1070). Voir R. Rashed et A. Djebbar, L'œuvre algébrique d'al-Khayyâm.
À la fin de l'an 1077, il achève son commentaire sur certaines prémisses problématiques du Livre d'Euclide, en trois chapitres.

Biographies

(en) Edward Granville Browne, A Literary History of Persia, vol. 2, London, T. F. Unwin, 1906 ; édition de 1956, p. 251 sqq [lire en ligne [archive]]
(en) Hazhir Teimourian, Omar Khayyam: Poet, Rebel, Astronomer, The History Press Ltd, 2007 (ISBN 9780750947152)

Études sur Khayyâm poète

Kilien Stengel, Poètes du vin, poètes divins, préface de Jean-Robert Pitte, Paris, collection Écriture, Éditions de l'Archipel 2012, 280 p.

Études sur Khayyâm mathématicien

Roshdi Rashed, Al-Khayyam mathématicien, en collaboration avec B. Vahabzadeh, Paris, Librairie Blanchard, 1999, 438 p. Version anglaise : Omar Khayyam. The Mathematician, Persian Heritage Series n^o 40, New York, Bibliotheca Persica Press, 2000, 268 p. (sans les textes arabes).
Roshdi Rashed, L’Œuvre algébrique d'al-Khayyam (en collaboration avec Ahmed Djebbar), Alep : Presses de l’Université d’Alep, 1981, 336 p.
Ahmed Djebbar, L'émergence du concept de nombre réel positif dans l'Épître d'al-Khayyâm (1048-1131)

Approches romanesques de Khayyâm

Amin Maalouf évoque Omar Khayyâm ainsi que Nizam al-Mulk et Hassan ibn al-Sabbah dans son roman Samarcande (1988).
Normand Baillargeon consacre à Omar Khayyâm son recueil mêlant prose et poésie intitulé: Le roman de Khayyam, Poète de Brousse, 2016.
Omar Khayyâm apparaît en filigrane dans le roman de Vladimir Bartol Alamut, compagnon de jeunesse de Hassan ibn al-Sabbah, le fondateur de la secte des Assassins.
Jacques Attali dans son roman La Confrérie des éveillés (2005) fait référence à Omar Khayyâm
Olivier Weber évoque Omar Khayyâm et sa ville de Nichapûr ainsi que les grands poètes persans dans son roman en forme de récit de voyage Le Grand Festin de l'Orient (2004).
Linda Lê dans son roman Les Trois Parques (éd Christian Bourgois, 1997) le cite à plusieurs reprises
Marjane Satrapi cite un poème de Khayyâm dans la bande dessinée Poulet aux prunes
Denis Guedj dans son roman retraçant l'histoire des mathématiques Le Théorème du Perroquet
Jean-Yves Lacroix : une biographie romancée d'Omar Khayyâm : Le Cure-dent, éd. Allia, (ISBN 978-2-84485-283-0)
Xavier Philiponet dans le récit Le Troisième Œil, Les Joueurs d'astres (avril 2010 - (ISBN 978-2-9531182-1-6)), consacre un chapitre entier à Omar Khayyâm et à Samarcande.
Dans son roman Le Loup des mers, Jack London fait connaître Omar Khayyâm au capitaine Loup Larsen par le narrateur. Trois jours durant, Humphrey récite les quatrains de Khayyâm à Larsen.
Jean Dytar fait de la rencontre rêvée entre Omar Khayyâm et Hassan ibn al-Sabbah la trame de sa bande dessinée Le sourire des marionnettes (Delcourt, 2009, (ISBN 978-2-7560-1378-7))
(en) Mehdi Aminrazavi, The Wine of Wisdom - The Life, Poetry and Philosophy of Omar Khayyam, Oneworld Oxford 2005.
(ar) Rubayyat Al-Khayam : œuvre du poète égyptien Ahmed Rami.

Le mathématicien prodige de Neyshâbour

Article rédigé par : Shahâb Vahdati

Souvent connu en tant que poète pour ses fameux quatrains, Omar Khayyâm était également un éminent mathématicien. Ses efforts notamment dans la résolution des équations algébriques auraient influencé René Descartes au XVIIe siècle dans la fondation de la géométrie analytique. Il est intéressant de voir que ces deux hommes ont eu plus que les mathématiques en commun. Descartes, théologien et recteur de l’Université d’Utrecht, fut accusé d’athéisme. Khayyâm avant lui, avait également risqué la persécution pour sa liberté de pensée notamment dans le domaine religieux.

Mathématiquement, la méthode cartésienne se situe dans le prolongement de la méthode de Khayyâm. Descartes découvre que certains points d’intersection peuvent représenter des racines imaginaires et il donne ainsi une solution complète pour les réponses négatives, positives et imaginaires.

Plus que pour son important traité sur l’algèbre, Khayyâm était davantage connu en Orient comme l’astronome qui a réformé le calendrier solaire iranien. Ce ne fut qu’au XIXe siècle que ses recherches algébriques commencèrent à être étudiées et découvertes, et c’est pour cette raison que ses travaux n’ont pas eu l’impact qu’ils auraient dû avoir dans le monde scientifique. Quand ses recherches attirèrent l’attention des savants, principalement au XIXe siècle, les sciences avaient déjà atteint un niveau plus élevé, de sorte que la connaissance de l’œuvre du savant iranien revêtait seulement une importance historique. L’historien américain des sciences George Sarton écrivit pourtant à son propos : « Khayyâm est le premier à s’être intéressé aux équations linéaires, carrées et cubiques. Il a présenté une catégorisation admirable des équations dont il a cherché les formes géométriques. Son traité d’algèbre introduit une pensée bien ordonnée. Ce traité est l’un des plus remarquables du Moyen-âge. »

En réalité, Khayyâm a effectivement contribué aux sciences, en particulier en réalisant une suite de découvertes dans le domaine des mathématiques, de l’astronomie et de la physique. Pour la première fois de l’histoire des mathématiques, il a donné une classification complète de tous les types d’équations, y compris des équations linéaires, carrées et cubiques. En élaborant une théorie systématique afin de trouver la solution des équations cubiques, il a fondé la théorie de la solution des équations algébriques.

Khayyâm a également travaillé sur la théorie mathématique de la musique en décrivant, en autres, la méthode d’extraction des degrés des entiers relatifs. Certains de ses travaux sont absolument remarquables pour leur époque. Sa définition de la physique est encore aujourd’hui un sujet d’actualité et de recherches, et une question importante de la science contemporaine. A titre d’exemple, Khayyâm avait notamment évoqué l’idée de l’existence de ce qu’on connaît aujourd’hui sous le nom de « masse noire ».


Omar Khayyâm trouva il y a environ neuf siècles
une solution géométrique à l’équation cubique en accédant à
un ensemble de nombres représentant
les coefficients binomiaux dans un triangle.

On utilise actuellement dans la plus grande partie du monde le calendrier grégorien, avec une erreur de vingt-six secondes dans le temps séculaire. Omar Khayyâm a conçu le sien avec une erreur de seulement douze secondes. Ce fut également lui qui annonça l’impossibilité de résoudre les équations cubiques en usant de règle et de compas, et résolut lui-même ces équations en ayant plutôt recours aux dessins géométriques basés sur les coniques.

Il a su trouver une solution générale aux équations carrées en utilisant les deux méthodes différentes d’une solution géométrique et arithmétique en même temps mais concernant les équations cubiques, il utilisa seulement les formes géométriques où il a étudié la possibilité d’existence de deux réponses à la fois. Le problème essentiel consistait dans le fait qu’à l’époque, on ne connaissait pas encore les réponses négatives et Khayyâm, par conséquence, n’y prêta aucune attention. De même, il évitait la possibilité d’obtenir trois réponses pour une équation cubique. Il réussit pourtant, quatre siècles avant Descartes, à achever l’une des plus grandes découvertes de la science en définissant le nombre comme une quantité continue, pour présenter le premier l’entier naturel et faire une démonstration selon laquelle toute quantité mathématique peut se diviser une infinité de fois. Il a également initié une conception bien ancrée en géométrie tout en recherchant un moyen pour démontrer l’axiome des parallèles ou le cinquième postulat d’Euclide.

Le triangle de Pascal

Omar Khayyâm trouva il y a environ neuf siècles une solution géométrique à l’équation cubique en accédant à un ensemble de nombres représentant les coefficients binomiaux dans un triangle, découverte attribuée à Pascal dans la tradition européenne. Pourtant, certains mathématiciens iraniens comme Al-Karaji (953-1029) ont même découvert cet ensemble bien avant Khayyâm, et en ont indiqué l’existence. Omar Khayyâm utilisa cet ensemble pour calculer le carré de la somme de deux nombres. Il trouva une démonstration pour la formule du binôme qu’il exprime dans son traité d’algèbre : « J’ai composé un livre afin d’expliquer la justesse des règles, nécessaires pour obtenir la réponse des équations cubiques et pour extraire le côté du carré, du cube, etc. Ces règles sont des nouveautés dans la science. Ces démonstrations sont arithmétiques. »

Il faut mentionner que les solutions mathématiques s’appuyaient jusqu’au XVIe siècle sur des méthodes géométriques et les mathématiciens, bien loin d’avoir accès aux symboles qui définissent une langue propice aux polémiques scientifiques, facilitant infiniment cette démarche, démontraient plutôt par un langage descriptif ordinaire. Ils résolvaient les problèmes avec des méthodes géométriques. La méthode descriptive peut être comprise de ce court fragment du traité d’algèbre de Khayyâm : « Maintenant, on présente des principes à l’aide desquels on peut trouver le nombre des monômes pour ceux dans d’autres formules du multinôme, quand un nombre se divise en deux. Comme base du travail, si tu veux ceci, mets l’« unité » sous l’« unité ». Ensuite, transmets l’ "unité" à la colonne suivante, ajoute l’« unité » qui se trouve sous la première « unité », Ce sera « deux ». Mets ce « deux » sous l’ "unité » et mets une « unité » sous le « deux ». Ce sera : « unité, deux, unité ». Cela te montre que le carré d’une somme de deux nombres est ainsi. Il faut multiplier chaque nombre en soi, car tu as aux deux côtés, l’« unité » et l’« unité » ; et tu dois multiplier deux fois un nombre à un autre, car tu as un « deux » au centre. Ainsi, tu achèveras le carré de ce nombre. Ensuite, transmets à nouveau le nombre à la colonne suivante, ajoute l’« unité » au « deux », tu achèveras « trois », écris ça sous l’« unité ». Ajoute le « deux » à l’« unité », tu achèveras le « trois ». Ecris cela sous le « trois ». Tu auras à la deuxième colonne : « unité, trois, trois, unité ». Ainsi tu pourras obtenir le cube de tout nombre, quand il a la forme de la somme de deux nombres ».

Dans son livre intitulé Discours sur les types des quarts sur la théorie de la musique, Khayyâm a procédé à une analyse mathématique de la musique, du problème de la division du quart d’une gamme à trois intervalles dans un système régulier.

Selon les renseignements disponibles à propos d’un traité perdu de Khayyâm dont le titre révèle quasiment le contenu La justesse des méthodes indiennes pour le calcul du cube et du carré, il est à dire qu’il a généralisé les méthodes indiennes pour calculer le carré et le cube d’un nombre donné. Khayyâm connaissait alors ce que l’on appelle la règle de Newton mais selon les documents historiques, les lois concernant les coefficients binômes et le triangle arithmétique – triangle de Pascal – remonterait à Karadji. Il a également résolu l’équation x3 + 200x = 20x2 + 2000 en donnant une racine positive avec l’intersection d’une hyperbole rectangulaire et un cercle. La solution numérique est trouvée approximativement par l’interpolation dans les tables trigonométriques. Il semblerait également qu’il ait conçu une théorie générale des équations cubiques dont la solution n’a pas besoin des sections coniques avec la méthode de la règle et du compas, une démarche qui sera prouvée en Europe 750 ans plus tard.


Première page d’un manuscrit du Traité sur les preuves des problèmes en algèbre

En ce qui concerne l’algèbre [1], l’œuvre de Khayyâm dans la création du théorème géométrique des équations cubiques est le travail le plus réussi accompli par un savant iranien. Ces équations ont absorbé les mathématiciens du IXe au XVIe siècle.

Les mathématiciens italiens Cardan et Tartaglia trouvèrent finalement une solution au XVIe siècle. D’autre part, Khayyâm a contribué de manière significative à la découverte de la racine positive par un argument géométrique, mais c’est seulement au XVIIe siècle que Descartes établit une relation entre la géométrie et l’algèbre. Khayyâm fut ainsi le premier à démontrer qu’une équation cubique peut avoir plus d’une seule réponse ou n’en avoir aucune.

La formule du binôme

Six cents ans avant le savant anglais Isaac Newton dont la formule porte le nom, Khayyâm est le premier a avoir présenté la formule du binôme pour les paramètres naturels dans son théorème des coefficients binominaux. Cette formule, que Newton a peut être extrait des travaux de Khayyâm, reproduite dans un langage scientifique moderne, décorée de signes et de symboles mathématiques, est ceci :

De 1074 à sa mort, Khayyâm supervisa la construction d’un grand observatoire astronomique à Ispahan, où il travailla ensuite et contribua à la réforme du calendrier solaire. En ce domaine, il fut celui qui donna la mesure de la durée de l’année de 365,24219858156 jours.

Liste des traités mathématiques d’Omar Khayyâm :

- Moshkilât al-Hisâb (Les difficultés de l’arithmétique)

- Traité algébrique sans nom.

- Risâla fi al-Barâhin al-Masâ’il al-Jabr wa al-Moqâbila (Traité sur les preuves des problèmes en algèbre)

- Sharh Moshkilât min Mosâdirât Kitâb Oqlidos (Explication sur les difficultés des définitions du livre d’Euclide)

- Jawâmi’ al-Hisâb (Encyclopédie de l’arithmétique).

- Al-Qawl ‘alâ Ajnâs al-lati bil-Arba’a (Discours sur les types des quarts)

Les travaux mathématiques de Khayyâm ont suivi trois directions : l’algèbre, la théorie des parallèles, la théorie des relations entre les entités arithmétiques ou les premières initiations avec la théorie des nombres. Dans tous ces domaines, Khayyâm eut des prédécesseurs et des successeurs importants, notamment dans les pays musulmans. Comme Aristote et Euclide, il avait commencé par l’apprentissage des œuvres classiques.

Références bibliographiques :
Shahriâri, Parviz, Târikh-e Riyâzidânân-e Mosâlmân (Histoire des matématiciens musulmans).
Mohâseb, Gholam Hossein, Resâleh-ye Khayyâm dar bâb-e elal dar jabr (Traité de khayyâm sur les causes en algèbre, Enteshârât-e Malek, Téhéran, 1999.
Arâni, Taghi, Resâleh-ye Khayyâm dar bâb-e Moshkelât-e Oqlidos (Traité de Khayyâm sur les difficultés d’Euclide), Téhéran, Enteshârât-e Jâvid, 1933.
Alishâhi, Ali, Sargozasht-e Riyâzidânân-e Irân va Jahân, Kholâseh yek Sokhanrâni dar Estânbul (Biographie des mathématiciens de l’Iran et du monde, extrait d’un discours à Istanbul), Revue Hebdomadaire Pouyâ, printemps 2003.

Notes

[1] Le dictionnaire Larousse définit l’algèbre comme la science du calcul des grandeurs représentées par des lettres. En langue arabe – que les savants persans utilisaient au Moyen-âge comme le latin en Europe pour des fins scientifiques – ce mot désigne « la réunion des parties cassées".

Neychapour - CIRCUITS EN IRAN

Suivi Perso

Guides

Hôtels

Neychapour